110. Rowland's Ring

Rowland's Ring is used to demonstrate the magnetization curve of iron. (See Halliday and Resnick, Part II, Sec. 37.6) We have an actual Ring, or the Leybold demountable transformer will serve.

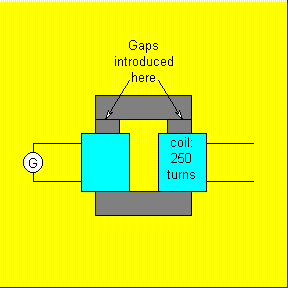
rwlndrng.gif (3590 bytes)

The flux in the iron is measured by switching off the current in the energizing coil and recording the reading of a ballistic galvanometer hooked to a pickup coil. (You can show that the maximum reading of a ballistic gavanometer is proportional to q = i t, which is in turn proportional to the change in flux through the pickup coil. You can determine the constant of proportionality by discharging a known capacitor through the galvanometers.) The large demonstration galvanometer will serve as a ballistic galvanometer for lecture purposes.

Professor J. Oostens has suggested the following demonstration of magnetic saturation and reluctance:

The Leybold transformer is arranged as above. The experiment is run first with no gap for several values of the current. Then a small gap is provided with shims, and the measurements repeated for the same set of currents. A Hall probe and Gaussmeter can be introduced in the second case for more accurate measurements of B in the gap. Sample data are shown below:

I

(amps)

 nI

(amp.turns)

 GFe

(units)

 GGap

(units)

 BCap

(Tesla)

<--higher degree of accuracy.
10 2500 1.2 1.3 0.89

Some deviation is due to a remiant field. (Iron behaves like a magnet for very low currents)
5 1250 1.1 0.75 0.50
3 750 0.95 0.45 0.28
2 500 0.8 0.27 0.19
1 250 0.7 0.1 0.090
0.5 125 0.45 0.05 0.012

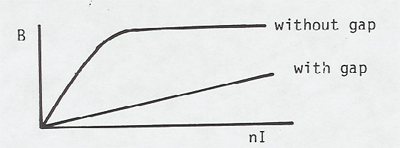
The graph shows that the field in the iron quickly reaches saturation. By computing the reluctance,

Reluctance = magnetomotive force / flux = nI / Φ

you can show that the reluctance of the air gap is much greater than that of the iron, even though the path length is much smaller.