- 1. Mechanics
- A. First Day Demos
- B. First Law, Inertia
- C. Second Law
- D. Third Law
- E. Angular Momentum
- F. Ballistics
- G. Center of Mass Demonstrations
- H. Energy
- I. Friction
- J. Gravitational Acceleration
- K. Kinematics
- L. Momentum and Collisions
- M. Nonlinear Mechanics
- N. Rotational Inertia
- O. Statics
- P. Torque
- Q. Uniform Circular Motion
- R. Vectors and Forces
- S. Data Studio
- 2. Harmonic Motion, Waves and Sound
- 3. Matter and Thermodynamics
- 4. Electricity and Magnetism
- 5. Light and Optics
- 6. Modern Physics
- 7. Astronomy
- 8. Software and Multimedia
- 9. Index and code conversion from older manual
- External Resources
30. Stacking Blocks
If a series of identical rectangular blocks is stacked out at their balancing points from the top down, the top block can stick out arbitrarily far. You can show with a simple center of mass calculation the total "stick-out" distance; that is, the horizontal distance from the back of the bottom block to the back of the top block is 1/2(1 + 1/2 + 1/3 + 1/4 + ...). This series grows without limit.
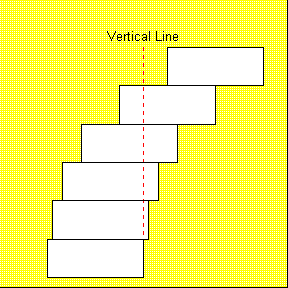
Many students are surprised to see the top block "sticking out in space", no part of it over the bottom block of the stack. The series above shows that this can happen with a stack of only 6 blocks. In practice at least 6 are needed, and several more to make to effect dramatic.
