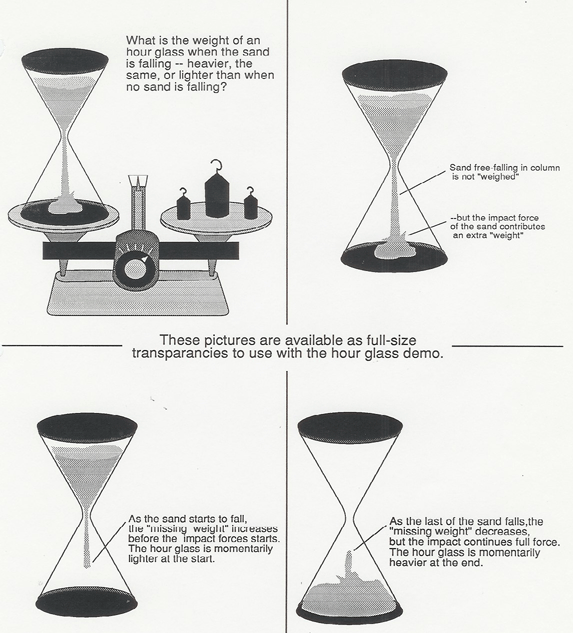
110. Weight of an Hourglass

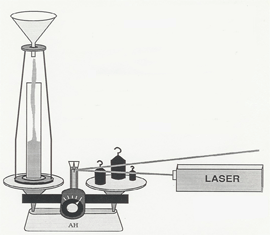
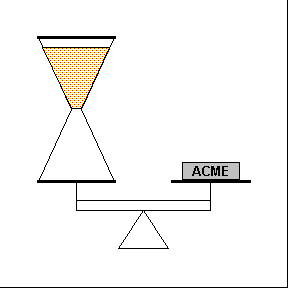
Does the weight of an hourglass change when the sand is falling? This demo shows the truth! A funnel with the sand held back by a cork and string arrangement is perched to drop sand into a glass beaker on a double pan balance. A laser bounces a beam off a small mirror attached to the pointer of the balance. When you burn the string, the sand starts falling, and the motion of the laser spot on the blackboard indicates the result. A set of transparencies to use with this demo is shown below.



 

The sand in the falling column does not contribute to the weight reading. But you can easily show from Newton's Second Law in the form F = dp/dt that the extra impact force of the falling sand exactly equals the missing weight of the total falling column of sand. Thus, while the sand is falling and impacting, the weight of the hourglass is equal to its weight when no sand is falling.

But initially, as the sand starts falling, there is "missing weight" in the column before the sand hits bottom, so the hourglass grows momentarily lighter. Similarly, at the end there a few moments while the impact force remains constant as the falling column decreases to zero, so the hourglass grows momentarily heavier. The movements of the laser spot on the blackboard faithfully trace out the graph of the weight of the hourglass as a function of time.


 

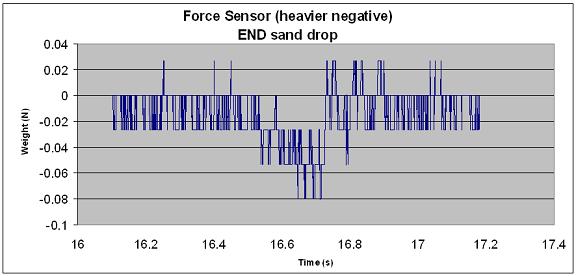
A movie clip of the typical setup is shown on the right. Note the position of the laser spot as the sand begins to drop and as its level in the funnel changes.


 

The graphs below were produced with data from a setup using a PASCO force sensor in place of the scale.