30. Special Relativity
"The influence of the crucial Michelson-Morley experiment on my own efforts has been rather indirect. I learned of it through H.A. Lorentz's decisive investigations of the electrodynamics of moving bodies (1895) with which I was acquainted before developing the special theory of relativity . . . What led me more or less directly to the special theory of relativity was the conviction that the electromotive force acting on a body moving in a magnetic field was nothing else than an electric field.
-Albert Einstein
Although most physicists are aware that relativity is involved in the Faraday magnet and coil induction experiment, few exploit the full significance of it as a relativity demonstration. But this experiment demonstrates a truly relativistic effect at very low velocities. It shows, among other things, that physical results depend only on the relative motion (Einstein's first postulate of relativity, the physics is independent of the uniform motion of an inertial frame), and that electric and magnetic fields manifest themselves differently to different moving observers. In addition the experiment has the advantage of motivating relativity in the same way as Einstein was motivated, as in the quote above. This demonstration is useful as a general introduction to relativity in the non-calculus courses and as a motivation for the Lorentz transformation in a higher level special relativity course.

A good place to introduce the demonstration for the first time is just before the coverage of Faraday Induction. (Later when relativity is covered, the demonstration can be repeated and new features emphasized. Referring to the figure first hold the magnet stationary with respect to the classroom, and move the coil toward the magnet. In this situation, case A, the force that moves the electrons around the coil to produce the galvanometer readings the Lorentz force F = qv/c X B. where v is the velocity of the coil toward the magnet.
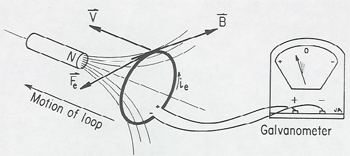
Before demonstrating the moving magnet case B, discuss with the students what they should expect to see. There is a magnetic field, but this does not affect the electrons in the coil, since their velocity is initially zero, and even after they begin to circulate around the coil, the magnetic v X B force is perpendicular to the wire and so does not cause the current. In fact, nothing the students have studied so far in E & M would lead them to expect a galvanometer reading in case B. When this proposition is put to the class, some students will object that " it shouldn't matter whether the coil or magnet is moved". If the class is pressed on this point, one can usually draw out the comment that "only the relative motion should matter". After a short discussion of Einstein's relativity principle, one can go on to perform case B. moving the magnet toward the coil. But, of course, although Einstein's postulate tells us that there must be a new force on the electrons, this new force must have a specific physical origin or description, and it is then appropriate to introduce Faraday induction or Grad X E = 1/c dB/dt. (In a non-calculus course this can be simply worded as a changing magnetic field produces a circular electric field.)
Further points that can be emphasized when the experiment is demonstrated later for relativity are:
- It is the relative motion that produces the same physical result in both cases A and B, a certain deviation of the galvanometer.
- In case A there is only a magnetic field in the classroom, but in case B there is also an electric field in the classroom. It is this electric field that is acting on the elections to cause the galvanometer deflection in case B. In the older texts the force owing to the electric field was called the electromotive force, as in Einstein's quote above.
- The demonstration shows the Lorentz transformation of the electromagnetic field in that in a frame moving through a stationary B field, there is also an E field.
- The galvanometer deflection is truly a relativistic effect, proportional to v/c. This is most easily seen in the cgs system from Maxwell's equation Grad X E = 1/c dB/dt with dB/dt proportional to v. It is interesting to ask the advanced students why a relativistic effect can easily be seen here even though v/c = 10-8. The reason is the same reason why a current carrying wire produces a measurable magnetic field (also a relativistic effect). The magnetic field of a single electron moving with velocity v is B = e/r3 v/c X r. Here the velocity is the drift velocity of the electrons v = 10-2 cm/sec, but the wire has lots of electrons.
The principles of this demonstration as presented in a non-calculus course are summarized on the next page which is available as a transparency from Art.
This demonstration was inspired by section 16.7 of Basic Physics by Kenneth W. Ford (Blaisdell Publishing Co., Waltham, Mass., 1968) The Einstein quote quote at the beginning was from the 1952 meeting honoring the centenary of Michelson's birth as quoted in Introduction to Special Relativity by Robert Resnick (John Wiley and Sons, New York, 1968).
(Art Huffman, AJP 48, 780 (1980))
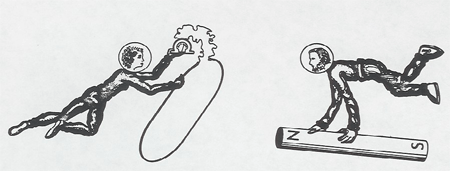
We see Lucy and Ringo both moving, approaching each other.
Lucy says:
The loop is stationary and the magnet is moving toward it. There is a magnetic field, but it can't produce any force on my electrons since they are stationary within the loop. Instead, the magnetic field is changing, growing stronger as the magnet gets closer, and this changing magnetic field produces an electric field which causes forces on the electrons, and drives them around the loop and produces the current in the galvanometer.
Ringo says:
The magnet is stationary and the loop is moving toward it. The electrons in the loop, since they are moving with the loop, feel a magnetic force, F = - e/c v X B, which drives them around the loop and produces the current in the galvanometer. There is no electric field.
The Conclusion:
Electric and magnetic fields are not invariant entities themselves, but are aspects of a single entity, the electromagnetic field, which manifests itself differently to different moving observers.
