Experiment 3 - Electrostatics

APPARATUS

• Heat lamp
• Timer
• Two Lucite rods
• Rough plastic rod
• Silk
• Cat fur
• Stand with stirrup holder
• Pith balls on hanger
• Electroscope
• Electrophorus
• Coulomb's Law (charging pads not needed)

INTRODUCTION

This experiment consists of many short demonstrations in electrostatics. In most of the exercises, you do not take data, but record a short description of your observations. If high-humidity conditions prevent you from completing certain parts, you may try them again next week with the Van de Graaff experiments.

THEORY

The fundamental concept in electrostatics is electrical charge. We are all familiar with the fact that rubbing two materials together — for example, a rubber comb on cat fur — produces a “static” charge. This process is called charging by friction. Surprisingly, the exact physics of the process of charging by friction is poorly understood. However, it is known that the making and breaking of contact between the two materials transfers the charge.

The charged particles which make up the universe come in three kinds: positive, negative, and neutral. Neutral particles do not interact with electrical forces. Charged particles exert electrical and magnetic forces on one another, but if the charges are stationary, the mutual force is very simple in form and is given by Coulomb's Law:

\begin{eqnarray} F_{\textrm{E}} &=& kqQ/r^2, \end{eqnarray}

where \(F_{\textrm{E}}\) is the electrical force between any two stationary charged particles with charges \(q\) and \(Q\) (measured in coulombs), \(r\) is the separation between the charges (measured in meters), and \(k\) is a constant of nature (equal to 9×10⁹ Nm²/C² in SI units).

The study of the Coulomb forces among arrangements of stationary charged particles is called electrostatics. Coulomb's Law describes three properties of the electrical force:

1. The force is inversely proportional to the square of the distance between the charges, and is directed along the straight line that connects their centers.

2. The force is proportional to the product of the magnitude of the charges.

3. Two particles of the same charge exert a repulsive force on each other, and two particles of opposite charge exert an attractive force on each other.

Most of the common objects we deal with in the macroscopic (human-sized) world are electrically neutral. They are composed of atoms that consist of negatively charged electrons moving in quantum motion around a positively charged nucleus. The total negative charge of the electrons is normally exactly equal to the total positive charge of the nuclei, so the atoms (and therefore the entire object) have no net electrical charge. When we charge a material by friction, we are transferring some of the electrons from one material to another.

Materials such as metals are conductors. Each metal atom contributes one or two electrons that can move relatively freely through the material. A conductor will carry an electrical current. Other materials such as glass are insulators. Their electrons are bound tightly and cannot move. Charge sticks on an insulator, but does not move freely through it.

A neutral particle is not affected by electrical forces. Nevertheless, a charged object will attract a neutral macroscopic object by the process of electrical polarization. For example, if a negatively charged rod is brought close to an isolated, neutral insulator, the electrons in the atoms of the insulator will be pushed slightly away from the negative rod, and the positive nuclei will be attracted slightly toward the negative rod. We say that the rod has induced polarization in the insulator, but its net charge is still zero. The polarization of charge in the insulator is small, but now its positive charge is a bit closer to the negative rod, and its negative charge is a bit farther away. Thus, the positive charge is attracted to the rod more strongly than the negative charge is repelled, and there is an overall net attraction. (Do not confuse electrical polarization with the polarization of light, which is an entirely different phenomenon.)

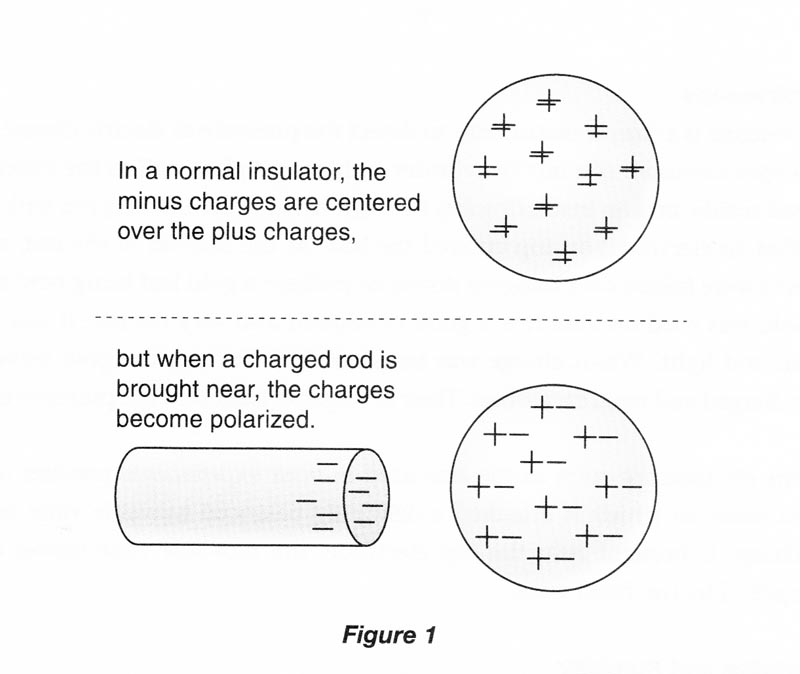
If the negative rod is brought near an isolated, neutral conductor, the conductor will also be polarized. In the conductor, electrons are free to move through the material, and some of them are repelled over to the opposite surface of the conductor, leaving the surface near the negative rod with a net positive charge. The conductor has been polarized, and will now be attracted to the charged rod.

Now if we connect a conducting wire or any other conducting material from the polarized conductor to the ground, we provide a “path” through which the electrons can move. Electrons will actually move along this path to the ground. If the wire or path is subsequently disconnected, the conductor as a whole is left with a net positive charge. The conductor has been charged without actually being touched with the charged rod, and its charge is opposite that of the rod. This procedure is called charging by induction.

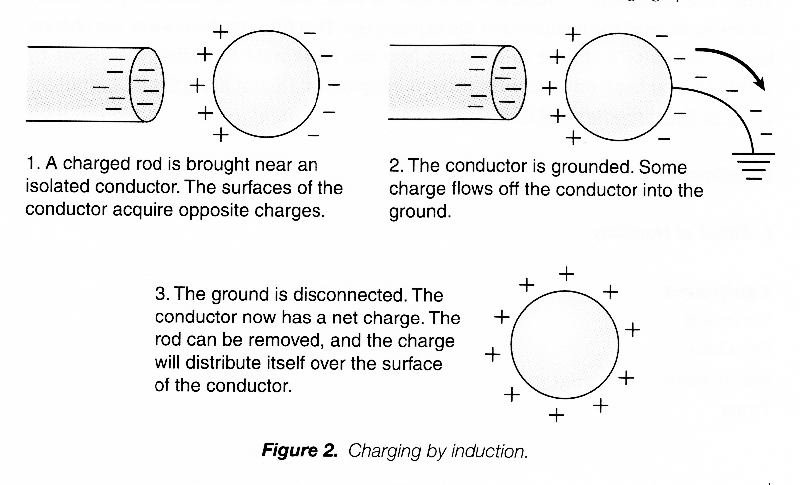
THE ELECTROSCOPE

An electroscope is a simple instrument to detect the presence of electric charge. The old electroscopes consisted of a box or cylinder with a front glass wall so the experimenter could look inside, and an insulating top through which a conducting rod with a ball or disk (called an electrode) on top entered the box. At the bottom of the rod, very thin gold leaves were folded over hanging down, or perhaps a gold leaf hung next to a fixed vane. Gold was used because it is a good conductor and very ductile; it can be made very thin and light. When charge was transferred to the top, the gold leaves would become charged and repel each other. Their divergence indicated the presence of charge.

A modern electroscope such as the one used in your experiments consists of a fixed insulated vane, to which is attached a delicately balanced movable vane or needle. When charge is brought near the top electrode, the movable vane moves outward, being repelled by the fixed vane.

ELECTROSTATICS AND HUMIDITY

We are all familiar with the fact that cold, dry days are “hot” for electrostatics, and we get small shocks after walking across a rug and touching a door knob, or sliding across a car seat and touching the metal of the car door. If the humidity is fairly low on the day of your lab, the experiments will proceed easily. If the humidity is extremely low, as is often the case in Southern California, you will probably not escape the lab without a direct experience with electrostatics! If the humidity is high, as it is sometimes in the summer, the experiments are more difficult, and some may be impossible.

If the experiments are difficult on the first week of the electrostatics lab, they will be left up so you can try some of them with the Van de Graaff experiments in the following lab.

When the air is humid, a thin, invisible film of water forms on all surfaces, particularly on the surfaces of the insulators in the experiment. This film conducts away the charges before they have a chance to build up. You can ameliorate this effect somewhat by shining a heat lamp on the insulators in the apparatus. Do not bring the heat lamp too close, or the insulators will be melted.

EXPERIMENTS

1. EFFECT OF HUMIDITY

   Equipment

   • Lucite rod
   • Silk cloth
   • Electroscope
   • Timer

   

   Procedure

   1. Record your observations in writing either on the computer (e.g., in Microsoft Word) or on your own paper. If writing by hand, write clearly, legibly, and neatly so that anyone, especially your TA, can read it easily. Start each observation with the section number and step number (e.g., I-2 for the step below). You do not need to repeat the question. Not all steps have observations to record.

   2. Record in your notes the relative humidity in the room (from the wall meter) and the inside and outside temperature.

   3. For this experiment, do not shine the flood lamp on the electroscope. Be prepared to start your timer. You may use the stopwatch function of your wristwatch.

   4. Rub the lucite rod vigorously with the silk cloth. Use a little whipping motion at the end of the rubbing. Touch the lucite rod to the top of the electroscope. Move the rod along and around the top so you touch as much of its surface to the metal of the electroscope as possible. Since the rod is an insulator, charge will not flow from all parts of the rod onto the electroscope; you need to touch all parts (except where you are holding it) to the electroscope. Start your timer immediately after charging the electroscope.

   5. Record the time it takes the electroscope needle to fall completely to 0°. Time up to five minutes, if necessary. If the needle has not fallen to 0° after five minutes, record an estimate of its angle at the five-minute mark. Typically, after charging, the needle might be at 80°.

      

   6. If the electroscope needle falls to 0° in a few minutes, the heat lamp will help in the experiments below. If the needle falls to 0° in 15 seconds or so, as it does on some summer days, you will probably have difficulty completing the experiments, even with the help of the heat lamp. If this is the case, you can try again next week.

2. ATTRACTION AND REPULSION OF CHARGES

   In this section, you will observe the characteristics of the two types of charges, and verify experimentally that opposite charges attract and like charges repel.

   Equipment

   • Two lucite rods
   • One rough plastic rod
   • Stand with stirrup holder
   • Silk cloth
   • Cat's fur

   

   Procedure

   1. Charge one lucite rod by rubbing it vigorously with silk. Place the rod into the stirrup holder as shown in Figure 7.

   2. Rub the second lucite rod with silk, and bring it close to the first rod. What happens? Record the observations in your notes.

   3. Rub the rough plastic rod with cat's fur, and bring this rod near the lucite rod in the stirrup. Record your observations.

   For reference purposes, according to the convention originally chosen by Benjamin Franklin, the lucite rods rubbed with silk become positively charged, and the rough plastic rods rubbed with cat's fur become negatively charged. Hard rubber rods, which are also commonly used, become negatively charged.

3. PITH BALLS

   In this section, you will observe the induced polarization of a neutral insulator and the transfer of charge by contact.

   Equipment

   • Hanger with pith balls
   • Lucite rod
   • Rough plastic rod
   • Silk cloth
   • Cat's fur

   

   Procedure

   (The heat lamp may help to minimize humidity near the pith balls.)

   1. Touch the pith balls with your fingers to neutralize any charge.

   2. Charge the lucite rod by rubbing it with silk.

   3. Bring the lucite rod close to (but not touching) the pith balls. Observe and record what happens to the balls. Explain your results. (Refer to the theory section, if necessary.)

   4. Touch the pith balls with your finger to discharge them. Recharge the lucite rod with silk.

   5. Touch the pith balls with the lucite rod. (Sometimes it is necessary to touch different parts of the rod to the balls.) Then bring the rod near one of the balls. What happens? Record and explain your results.

   6. Charge the rough plastic rod with cat's fur. How does the plastic rod affect the pith balls after they have been charged with the lucite rod? Record your results.

4. CHARGING BY INDUCTION

   Equipment

   • Electroscope
   • Lucite rod
   • Rough plastic rod
   • Silk cloth
   • Cat's fur

   

   Procedure

   1. Charge the lucite rod by rubbing it with silk.

   2. Bring the lucite rod near (but not touching) the top of the electroscope, so that the electroscope is deflected.

   3. Remove the lucite rod. What happens? Record the results your notes. Use several sentences and perhaps a diagram or two to explain the behavior of the charges in the electroscope.

   4. Bring the lucite rod near the electroscope again so that it is deflected. Hold the rod in this position, and briefly touch the top of the electroscope with your other finger. Keep the rod in position. What happens? Record the results in your notes.

   5. Now remove the lucite rod. If you have done everything correctly, the electroscope should have a permanent deflection. Diagram in your notes what happened with the charges. (Refer to the theory section, if necessary.)

   6. With the electroscope deflected as a result of the operations above, bring the charged lucite rod near the electroscope again. Remove the lucite rod, and bring a charged rough plastic rod near the electroscope. What happens in each case? Record the results in your notes.

5. ELECTROPHORUS

   The electrophorus is a simple electrostatic induction device invented by Alessandro Volta around 1770. Volta characterized it as “an inexhaustible source of charge”. In its present form, the electrophorus consists of a lucite plate on which rests a flat metal plate with an insulating handle.

   The lucite plate is positively charged by being rubbed with silk. Because lucite is an insulator, it remains charged until the charge leaks off slowly. The metal plate does not pick up this positive charge, even though it rests on the lucite. The plate actually makes contact with the lucite in only a few places; and because lucite is an insulator, charge does not transfer easily from it. Instead, when you touch the metal plate, electrons from your body (attracted by the positive lucite plate) flow onto the metal plate. Your body thus acts as an “electrical ground”. The metal plate is negatively charged by induction. Because the positive charge is not “used up”, the metal plate can be charged repeatedly by induction.

   Equipment

   • Electrophorus
   • Silk cloth
   • Electroscope
   • Neon tube

   

   Procedure

   (The heat lamp shining on the equipment may improve its operation.)

   1. Charge the electrophorus lucite plate by rubbing it with silk. A whipping motion toward the end of the rubbing may help. Usually the lucite needs to be charged only once for the entire experiment.

   2. Place the metal plate on the center of the lucite plate, and touch it with your finger. (You may feel a slight shock.)

   3. Hold the metal plate by its insulating handle as far from the metal as possible. Bring the metal to within 2 cm of your knuckle, and then slowly closer until a (painless) spark jumps.

   4. Recharge the metal plate by placing it back on the lucite, touching the lucite, and then lifting the plate off with its insulating handle. Bring it near your lab partner's knuckle.

   5. Repeat the procedure until you have experienced several sparks. What is the average distance a spark will jump? Record this distance in your notes.

   6. Recharge the metal plate, and bring it slowly near the top of the electroscope. Observe what happens with the electroscope needle.

   7. Move the plate away from the electroscope, and record what happens with the electroscope needle. Is it still deflected? Why or why not?

   8. Recharge the metal plate, and actually touch it to the top of the electroscope. Set the metal plate aside. Observe what happens with the electroscope needle. Is there any difference in the behavior of the needle compared to the results in procedure 6? If so, how do you account for the difference? Record this explanation in your notes.

   9. Once again, recharge the metal plate. Hold one end of the neon tube with your fingers, and bring the metal plate slowly closer to the other end. Observe what happens with the neon tube. The induced current should create a brief flash of light. By grounding the end of the tube with your fingers, you are providing a pathway for the charges to move.

   10. In this section, you charged the lucite plate by rubbing it at the beginning, and were then able to charge the metal plate repeatedly. Where does the charge on the metal plate come from? Where does the energy that makes the sparks and lights the tube come from? Comment in your notes.

6. COULOMB'S LAW

   You will be testing the inverse \(r\)-squared dependence of Coulomb's Law with a very simple apparatus. There is a tall box containing a hanging pith ball covered with a conducting surface, and similar pith balls on sliding blocks. A mirrored scale permits you to determine the position of the balls. (The purpose of the closed box is to minimize the effects of air currents.)

   

   The displacement \(d\) of the hanging ball from its equilibrium position depends on the electrical force \(F\) which repels it from the sliding ball. The force triangle of Figure 10 gives

   \begin{eqnarray} \tan\phi &=& F/mg, \end{eqnarray}

   while the physical triangle of the hanging ball gives

   \begin{eqnarray} \sin\phi &=& d/L. \end{eqnarray}

   

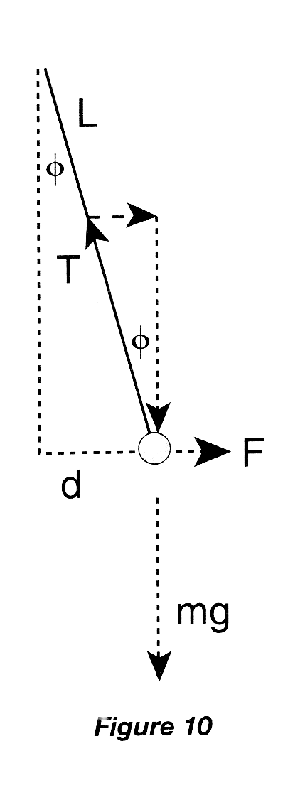
   If the angle \(\phi\) is small, then \(\tan\phi = \sin\phi\), and \(d\) is proportional to \(F\). Therefore, to demonstrate the inverse \(r\)-squared dependence of Coulomb's Law, we need to measure the displacement as a function of the separation between the centers of the balls.

   The purpose of the mirror is to minimize parallax errors in reading the scale. For example, to measure to position of the front of the hanging ball, line up the front edge of the ball with its image. Your eye is now perpendicular to the scale, and you can read off the position. Figure 11 below shows the situation where your eye is still too high and to the right.

   

   Equipment

   • Coulomb's Law apparatus
   • Electrophorus
   • Silk cloth

   Procedure

   1. Take a moment to check to position of the hanging ball in your Coulomb apparatus. Look in through the side plastic window. The hanging ball should be at the same height as the sliding ball (i.e., the top of the mirrored scale should pass behind the center of the hanging pith ball, as in Figure 12 below). Lift off the top cover and look down on the ball. The hanging ball should be centered on a line with the sliding balls. If necessary, adjust carefully the fine threads that hold the hanging ball to position it properly.

   2. Charge the metal plate of the electrophorus in the usual way by rubbing the plastic base with silk, placing the metal plate on the base, and touching it with your finger.

   3. Lift off the metal plate by its insulating handle, and touch it carefully to the ball on the left sliding block.

   4. Slide the block into the Coulomb apparatus without touching the sides of the box with the ball. Slide the block in until it is close to the hanging ball. The hanging ball will be attracted by polarization, as in Section III of this lab. After it touches the sliding ball, the hanging ball will pick up half the charge and be repelled away. Repeat the procedure if necessary, pushing the sliding ball up until it touches the hanging ball.

   5. Recharge the sliding ball so it produces the maximum force, and experiment with pushing it toward the hanging ball. The hanging ball should be repelled strongly.

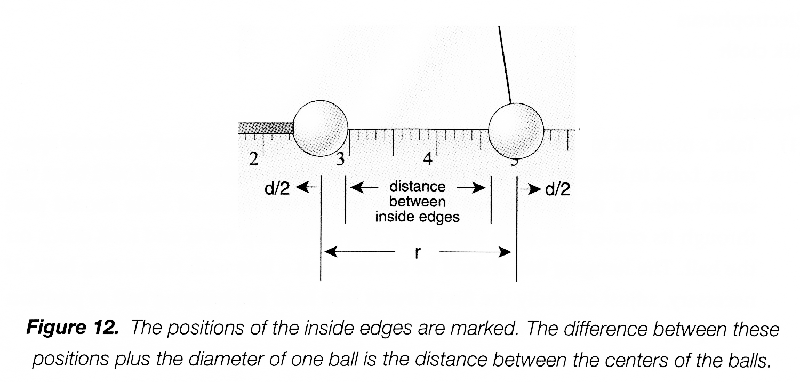
   6. You are going to measure the displacement of the hanging ball. You do not need to measure the position of its center, but will record the position of its inside edge. Remove the sliding ball and record the equilibrium position of its inside edge that faces the sliding ball, which you will subtract from all the other measurements to determine the displacement \(d\).

   7. Put the sliding ball in, and make trial measurements of the inside edge of the sliding ball and the inside edge of the hanging ball. The difference between these two measurements, plus the diameter of one of the balls, is the distance \(r\) between their centers. Practice taking measurements and compare your readings with those of your lab partner until you are sure you can do them accurately. Try to estimate measurements to 0.2 mm.

      

   8. Take measurements, and record the diameter of the balls (by sighting on the scale).

   9. Remove the sliding ball, and recheck the equilibrium position of the inside edge of the hanging ball.

   10. You can record and graph data in Excel or by hand (although if you work by hand, you will lose the opportunity for 2 mills of additional credit below). Recharge the balls as in steps 1 – 4, and record a series of measurements of the inside edges of the balls. Move the sliding ball in steps of 0.5 cm for each new measurement.

   11. Compute columns of displacements \(d\) (position of the hanging ball minus the equilibrium position) and the separations \(r\) (difference between the two recorded measurements plus the diameter of one ball).

   12. Plot (by hand or with Excel) \(d\) versus \(1/r^2\). Is Coulomb's Law verified?

   13. For an additional credit of 2 mills, use Excel to fit a power-law curve to the data. What is the exponent of the \(r\)-dependence of the force? (Theoretically, it should be −2.000, but what does your curve fit produce?)

   14. For your records, you may print out your Excel file with a table and graph of your numerical observations and any other electronic files you have generated.

ADDITIONAL CREDIT (3 mills)

You can change the charge on the sliding ball by factors of two, by touching it to the other uncharged sliding ball (ground it with your finger first). The balls will share their charge, and half the charge will remain on the first ball (assuming the balls are the same size). This way, you can obtain charges on the first ball of \(Q\), \(Q/2\), \(Q/4\), and so forth.

Devise and execute an experiment to verify the dependence of the Coulomb force on the value of one of the charges. (That is, we want to show that the force is proportional to one of the charges.) The method is up to you; explain your plan and results in your notes. What should you plot against what? Does anything need to be held constant?