Experiment 6 - The Charge-to-Mass Ratio of the Electron
APPARATUS
- Kent \(e/m\) Experimental Apparatus Model TG-13
- GW Laboratory DC Power Supply Model GPS-1850
- Heathkit Regulated Power Supply Model PS-4
- Triplett Multimeter Model 4000
- Simpson Digital Multimeter Model 464
- Bell 620 Gaussmeter with Hall Probe
- Magnetic compass
INTRODUCTION
Measuring separately the electric charge (\(e\)) and the rest mass (\(m\)) of an electron is a difficult task because both quantities are extremely small (\(e\) = 1.60217733×10-19 coulombs, \(m\) = 9.1093897×10-31 kilograms). Fortunately, the ratio of these two fundamental constants can be determined easily and precisely from the radius of curvature of an electron beam traveling in a known magnetic field. An electron beam of a specified energy, and therefore a specified speed, may be produced conveniently in an \(e/m\) apparatus. The central piece of this apparatus is an evacuated electron-beam bulb with a special anode. A known current flows through a pair of Helmholtz coils and produces a magnetic field. The trajectory of the speeding electrons moving through the magnetic field is made visible by a small amount of mercury vapor.
THEORY
An electron moving in a uniform magnetic field travels in a helical path around the field lines. The electron's equation of motion is given by the Lorentz relation. If there is no electric field, then this relation can be written as
\begin{eqnarray} \textbf{F}_B &=& -e(\textbf{v}\times\textbf{B}), \label{eqn_1} \end{eqnarray}
where \(\textbf{F}_B\) is the magnetic force on the electron, \(-e\) = -1.6×10-19 coulombs is the electric charge of the electron, \(v\) is the velocity of the electron, and \(\textbf{B}\) is the magnetic field. In the special case where the electron moves in an orbit perpendicular to the magnetic field, the helical path becomes a circular path, and the magnitude of the magnetic force is
\begin{eqnarray} F_B &=& evB. \label{eqn_2} \end{eqnarray}
Recall from Physics 6A that an object traveling around a circle experiences a centripetal force. For an electron of mass m moving at speed \(v\) in a circle of radius \(R\), the magnitude of the centripetal force \(F_C\) is
\begin{eqnarray} F_C &=& mv^2/R. \label{eqn_3} \end{eqnarray}
Therefore,
\begin{eqnarray} evB &=& mv^2 /R, \end{eqnarray}
or
\begin{eqnarray} eB &=& mv/R. \label{eqn_4} \end{eqnarray}
The initial potential energy of the electrons in this experiment is \(eV\), where \(V\) is the accelerating voltage used in the electron-beam tube. After the electrons are accelerated through a voltage \(V\), this initial potential energy is converted into kinetic energy \((1/2)mv^2\). Since energy is conserved, it follows that
\begin{eqnarray} eV &=& (1/2)mv^2. \label{eqn_5} \end{eqnarray}
Combining Eqs. 4 and 5 yields
\begin{eqnarray} e/m &=& 2V/B^2 R^2. \label{eqn_6} \end{eqnarray}
THE \(e/m\) APPARATUS
The electron-beam bulb used in this experiment has a cathode that is heated indirectly, a collimating grid with a hole, and an anode with a hole.
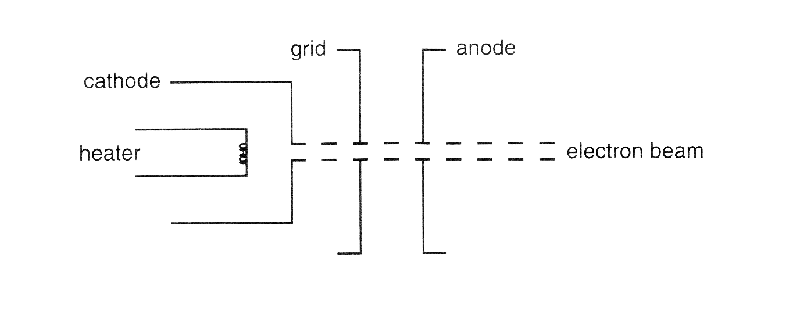
Electrons leave the heated cathode and are attracted by the anode, which has a positive potential with respect to the cathode. Most electrons are stopped by the collimating grid and the anode. Those that are able to pass through the hole in the anode emerge from the back of the anode as a thin, monochromatic beam. The kinetic energy of the electrons in this beam is equal to the potential energy difference between the anode and the cathode.
To make the path of the electrons visible, we use the following method. The large evacuated glass bulb that houses the cathode and anode is spiked with a trace of mercury, enough to produce nearly saturated mercury vapor with a small pressure of approximately 1×10-3 mm Hg. (By comparison, recall that normal atmosphere pressure is approximately 760 mm Hg.) Occasionally an electron from the beam with a kinetic energy of about 300 eV collides with a mercury atom, causing the atom to become excited — a process that requires 10.4 eV of energy. The excited atom then decays quickly back to the ground state, emitting several photons in the process (including the one that has the characteristic blue color of mercury light). Thus, the blue halo in the glass bulb marks the path of the electrons. Note that the electron-beam tube, along with its socket, can be rotated nearly 90°.
The Helmholtz coils consist of a pair of identical circular coils of wire, each of radius \(r\), connected in series.

The distance between the coils is denoted \(L\). When \(L \ll r\), the coils produce a nearly uniform magnetic field in the space between them.
Along the axis of one thin coil with \(N\) turns at a distance \(x\) from the plane of the coil, the magnitude of the magnetic field \(B\) due to a current \(I\) is
\begin{eqnarray} B &=& \mu_0 r^2 N I/[2(r^2+x^2)^{3/2}]. \label{eqn_7} \end{eqnarray}
The direction of the magnetic field is perpendicular to the plane of the coil, and its unit is the tesla (T), with 1 tesla = 104 gauss. In SI units, the magnetic permeability μ0 of free space is
\begin{eqnarray} \mu_0 &=& 4\pi\times 10^{-7} \textrm{ Tm/A}. \end{eqnarray}
For a pair of identical parallel coils separated by a distance \(L\), the magnitude of the magnetic field at a point along the \(x\)-axis is
\begin{eqnarray} B &=& [\mu_0 r^2 NI/2] [ 1/(r^2+x^2)^{3/2} + 1/(r^2+(L-x)^2)^{3/2} ]. \label{eqn_8} \end{eqnarray}
When \(x = L/2 \), Eq. \eqref{eqn_8} gives
\begin{eqnarray} B &=& \mu_0 r^2 NI/(r^2+L^2/4)^{3/2}. \label{eqn_9} \end{eqnarray}
EQUIPMENT
The centerpiece of this experiment is the Kent \(e/m\) Experimental Apparatus Model TG-13, which consists of the electron-beam bulb (EBB) and a pair of Helmholtz coils (HC). There is also an illuminated ruler behind the EBB to facilitate the measurement of the electron-beam radius. The apparatus is fed by three external power sources. The accelerating voltage for the EBB is produced by a Heathkit Regulated Power Supply Model PS-4. A voltage of 150 – 300 V at a modest current of approximately 50 mA is required. This supply also provides the cathode heater power using a 6.3-V alternating current. The electric current and voltages are measured with two digital multimeters: the Triplett Multimeter Model 4000 and Simpson Digital Multimeter Model 464.
We use a GW Laboratory DC Power Supply Model GPS-1850 for the HC, which also supplies the voltage for the small light bulb of the illuminated scale. A large current of 1 – 2 A is needed, but a low voltage of 5 – 15 V is adequate. The \(e/m\) apparatus may be covered with a black cloth to reduce background light.
INITIAL SETUP
On the front panel of the \(e/m\) apparatus are jacks for the power and the voltmeter, two control knobs, and a switch. Starting from the left side of the panel, we have:

-
Two jacks (A) for the connection to the Helmholtz coils (HC) power supply. The current is measured by a multimeter connected in series with the power supply.
-
A current adjustment knob (B) for the HC. (The current can also be changed directly by a knob on the power supply.)
-
The focus knob (C), which allows sharpening of the electron beam by variation of the voltage on the grid of the EBB. The grid is internally connected and does not need a separate power supply.
-
A switch (D). This should be set in the “e/m Measure” position.
-
Two jacks (E) for the voltmeter, which measures the accelerating voltage.
-
Two jacks (F) for the deflection plates. (These are not used.)
-
Two jacks (G) for the high-voltage (~300 V) input to the electrodes of the electron gun.
-
Two jacks (H) for connecting the electron-gun heater to the power supply which can be 6.3-V DC or AC. (We use AC.)
Connect the EBB to the power supplies and multimeters (see the figure below).

Use red cables for positive voltage and black cables for ground. To measure the HC current, make sure it passes through the Triplett multimeter in the current mode. (The HC power supply, the ammeter, and the HC are therefore connected in series.) Plug in the power supplies and the multimeters. Set the Triplett multimeter to the highest current scale, and put it in the DC-A mode. Connect the Simpson multimeter to the jacks labeled for the voltmeter (item E on the front panel of the EBB) set to the highest voltage scale, and put it in the DC-V mode.
PROCEDURE
-
Orient the Helmholtz coils (HC) so as to eliminate the influence of the Earth's magnetic field on the experiment. To do this, use a magnetic compass to determine the direction of the Earth's field, mark its direction on your work station with paper tape, and record its coordinates. Also measure and record the dip angle. Rotate the coils such that the plane of the HC lies in the plane of the Earth's magnetic field. With this orientation, the effect of the Earth's field on the HC is zero.
-
Connect the power supplies and multimeters to the \(e/m\) apparatus, as detailed in the previous section. Check that the polarities agree with the ones marked on the front panel of the apparatus.
-
Place the black cloth over the HC for easy observation of the electron beam. Turn on the heater supply, and allow two minutes for the filament to heat up. Apply 150 V to the anode, which should produce a visible beam. Turn on the current through the HC, and observe how the electron beam is bent and forms a circle.
-
Very carefully, rotate the glass bulb and observe the helical path of the electrons. Notice the direction of the helical axis.
-
Rotate the glass bulb such that the plane of the electron beam is exactly parallel to the plane of the HC. Using the focus control, obtain a well-defined beam. (You may also need to adjust the filament power to accomplish this.) If necessary, make a fine adjustment of the EBB's orientation so that the beam, after traveling a full circle, passes between the two metal struts which feed the power to the filament.
-
Set the HC current at a fixed value (e.g., 1 A). Measure \(R\) (the radius of the electron beam) for at least four settings of \(V\) (the accelerating voltage). Since \(e/m\) is proportional to \(1/R^2\), you should make an effort to measure \(R\) with small uncertainty. Use the mirror behind the EBB to minimize parallax. You may add a second ruler that is taped to the front of the HC.
-
Set the accelerating voltage at a fixed value (e.g., 200 V). Measure \(R\) for at least four settings of \(I\) (the HC current).
The manufacturer of the \(e/m\) apparatus did not supply the number of windings, \(N\), of the HC. On the front panel of the EBB stand, it is stated that \(B\) = (7.8 \(I\)) gauss, but no uncertainty is given. To determine the magnitude of the magnetic field, you will use a calibrated magnetometer (Bell 620 Gaussmeter) based on a calibrated Hall Probe.
Your TA will remove the EBB. Install the Hall-Probe holder in the HC. Calibrate the magnitude of the magnetic field \(B\) in the center of the HC for the four values of the current \(I\), including two different scale settings. Plot \(B\) as a function of \(I\). Note that the error in \(e/m\) is proportional to \(1/B^2\) (see Eq. \eqref{eqn_6}). Use the \(B\) versus \(I\) graph to determine the magnetic field for each value of the current.
-
Plot \(V\) as a function of \(R^2\) (the data in step 6), and use the slope of the graph to determine the ratio \(e/m\) with the help of Eq. \eqref{eqn_6}.
-
Plot \(I^2\) as a function of \(1/R^2\) (the data in step 7), and use the slope of the graph to determine the ratio \(e/m\) with the help of Eq. \eqref{eqn_6}.
-
Compute the ratio \(e/m\) using the “accepted” values provided in the “Introduction” section of this experiment, and compare it with your measured ratios from parts 8 and 9.
DETERMINATION OF THE ACCELERATION VOLTAGE
The absolute calibration of a voltage meter is a very difficult task. Traditionally, one uses standard cells which are stored at the National Calibration Laboratory in various countries. A new method depends on the so-called Josephson effect. We will assume that the multimeters have been calibrated sufficiently well. However, we should compare the voltage readings of the two multimeters to estimate the minimal value for the absolute error.
DATA
-
Coordinates of Earth's magnetic field =
Dip angle =
-
\(V\) (Trial 1) =
\(R\) (Trial 1) =
\(V\) (Trial 2) =
\(R\) (Trial 2) =
\(V\) (Trial 3) =
\(R\) (Trial 3) =
\(V\) (Trial 4) =
\(R\) (Trial 4) =
-
\(I\) (Trial 1) =
\(R\) (Trial 1) =
\(I\) (Trial 2) =
\(R\) (Trial 2) =
\(I\) (Trial 3) =
\(R\) (Trial 3) =
\(I\) (Trial 4) =
\(R\) (Trial 4) =
\(B\) (Trial 1) =
\(B\) (Trial 2) =
\(B\) (Trial 3) =
\(B\) (Trial 4) =
Plot the graph of \(B\) as a function of \(I\) using one sheet of graph paper at the end of this workbook. Remember to label the axes and title the graph.
-
Plot the graph of \(V\) as a function of \(R^2\) using one sheet of graph paper at the end of this workbook. Remember to label the axes and title the graph.
Slope of graph =
\(e/m\) =
-
Plot the graph of \(I^2\) as a function of \(1/R^2\) using one sheet of graph paper at the end of this workbook. Remember to label the axes and title the graph.
Slope of graph =
\(e/m\) =
-
\(e/m\) (computed from accepted values provided in “Introduction”) =
Percentage difference between experimental and accepted \(e/m\) from part 8 =
Percentage difference between experimental and accepted \(e/m\) from part 9 =
