- 1. Mechanics
- 2. Harmonic Motion, Waves and Sound
- 3. Matter and Thermodynamics
- 4. Electricity and Magnetism
- 5. Light and Optics
- A. Geometrical Optics
- 10. Blackboard Optics
- 20. Image From a Lens or Mirror
- 30. Introducing the Laser
- 40. Lens Aberrations
- 50. Measuring a Glasses Prescription
- 60. Multiple Images in Mirrors
- 70. Projected Colors
- 80. Real and Virtual Image Illusions
- 90. Refraction
- 100. Sunset Colors from Scattering
- 110. Total Internal Reflection
- B. Interference and Diffraction
- C. Optical Instruments
- D. Polarization
- E. Spectra
- F. Speed of Light
- A. Geometrical Optics
- 6. Modern Physics
- 7. Astronomy
- 8. Software and Multimedia
- 9. Index and code conversion from older manual
- External Resources
50. Measuring a Glasses Prescription
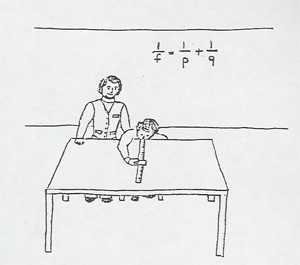
The near (pn) and far (pf) focusing distances of a student volunteer and his/her glasses prescription computed. The impressive thing about this demonstration is that you pay the optometrist $25 for the same service!
To measure the near and far focusing distances without danger of poking a ruler in the volunteer's eye, lay the ruler or meter stick on a lecture table with it's end at the edge of the table.. A volunteer should be chosen who is nearsighted without serious astigmatism (glasses diverging and rotationally symmetric). The volunteer is seated at the table and places his eye at the end of the ruler. Using a 3 X 5 card with fine print, the volunteer quickly determines the nearest and furthest distance he can focus clearly on it.
Without justifying the steps, the calculation goes as follows:
q = optical path length of eyeball, this is fixed for a particular individual and is unknown.
ff = focal length of eye lens and cornea with muscles relaxed.
fn = focal length of eye lens and cornea with muscles max contracted.
fg = focal length of glasses (to be determined).
Then,
1/ff = 1/q + 1/pf
The glasses should correct the far point to infinity, so
1/ff + 1/fg= 1/q + 1/infinity
Subtracting,
pg = 1/fg = -1/pf
Will the "patient" be able to read with these glasses on? Compute his near focusing distance pn' with glasses on.
1/fg + 1/fn = 1/q + 1/pn
Thus,
1/pn' = 1/fg + 1/pn
The quantity pn' should be less than 25 cm for easy reading. Otherwise the "patient" will need reading glasses or bifocals.
The power of accommodation can also be computed.
POA = pn - pf = 1/fn - 1/ff = 1/pn - 1/pf
In the farsighted case the person's far point will be beyond infinity, so to speak; that is, his eye will not focus at any finite distance, when relaxed. To handle this case, introduce a converging lens of known power pc = 1/fc at the person's eye. (The power should be chosen to bring his far point in to an easily measured distance, half a meter or less.) Then measure the near and far point through the converging lens. The equations are now
1/ff + 1/fc = 1/q + 1/pf
and
1/fn + 1/fc = 1/q + 1/pn
and fg can be computed as before from the known value of fc.
This demonstration was inspired by Chapter 26 of College Physics by Franklin Miller, Jr. (Harcourt Brace Jovanovich, New York, 1977).
(Art Huffman, A.J.P. 48, 309 (1980))
